Приветствую постоянных читателей и гостей сайта! Евдокс Книдский – это древнегреческий математик, механик, астроном, географ, лекарь, философ, музыкант, оратор и законовед. Надеюсь, что эта статья о гениальном ученом вам будет интересна.
Contents
Биография Евдокса Книдского
Очень давно, еще но нашей эры, в городе Книде родился один из самых выдающихся ученых Древней Греции.
Евдоксу было 23 года, когда он приехал в Афины слушать лекции в Академии великого Платона. Над входом в Академию было выгравировано известное изречение: «Пусть не входит сюда тот, кто не обучен математике».
Здесь он решил предложенную Платоном сложную астрономическую задачу. Создал модель, в которой движение Солнца, Луны и планет подавалось как союз равных круговых движений сфер. В центре была Земля. Модель Евдокса означала начало новой эры в истории астрономии.
Затем была поездка в Египет. Евдокс общался с местными жрецами, чтобы проникнуть в полученные ими закономерности движения небесных светил, тайны мироздания, числовые отношения.
Вернувшись, ученый основал в городе Кизика, на берегу Мраморного моря, школу математиков и астрономов. Там он оборудовал одну из лучших для своего времени астрономическую обсерваторию. Здесь проводили астрономические наблюдения, благодаря которым был составлен первый в стране звездный каталог.
В 365 г. до н.э. он во второй раз, теперь со своими учениками, посетил Афины. Он имел продолжительные беседы с Платоном на различные научные, прежде всего, философские темы.
Авторитет и слава ученого привлекали к нему многочисленных учеников. Им он передавал полученные знания, разрабатывал вместе с ними новые научные проблемы, воспитывая новых исследователей. Евдокс Книдский умер на 53-м году жизни в родном Книде, получив заслуженные славу и почести. Были у него три дочери и сын.
Вклад в науку Евдокса Книдского
Ни одна из работ Евдокса не сохранилась до наших дней. Поэтому историкам науки пришлось провести колоссальную работу, чтобы из книг других авторов, попутных упоминаний, выявить его вклад в науку.
На первый взгляд может показаться, что математик открывает и показывает свои теоремы независимо от событий окружающего мира. Биографии большинства математиков, включая Евдокса, убеждают нас в том, что это не так.
Чтобы понять стимулы математических поисков Евдокса, достаточно хотя бы бегло ознакомиться с обстановкой в греческой математике того времени.
Открытие несоизмеримости нанесло сокрушительный удар пифагорейской философии всесилия положительного рационального числа.
Математики еще жили под гнетом этой неожиданности, когда философ Зенон Элейский сформулировал свои 45 апорий. В них он показал противоречивость понятий движения, пространства и времени, бесконечности и непрерывности, а также трудности выражения движения в логике понятий.
Открытие несоизмеримых отрезков и апории Зенона Элейского обусловили первый кризис методологических основ математики. Они показали, что некоторые важные математические понятия требуют более глубокого изучения, уточнения, а теоретические основы всей математики — перестройки и укрепления.
Решению этих проблем, которые в настоящее время принадлежат математическому анализу, посвятил свой математический гений Евдокс Книдский. Он создал новые теоретические основы математики. Прежде всего общее учение об отношении, которое в основном совпадает с теорией действительных чисел.
Близкую к ней систему построил только в 1872 году немецкий математик Дедекинд (1831 -1916). Он открыл строгие методы предельных переходов. С их помощью удалось решить много задач на вычисление площадей. Это был знаменитый «метод исчерпывания».
Евдокс также был автором метода доказательства. В XVII в. его назвали «аподиктическим», или «методом сведение к абсурду».
Умные греки!
Греческие математики разработали два пути преодоления кризиса теоретических основ своей науки.
Демокрит из Абдер (ок. 460-370 до н. э.) предлагал рассматривать точки как неделимые атомы. Причем в каждом отрезке их всегда конечное, хотя и чрезвычайно большое число, когда плоскость образована из прямых, вроде того, как ткань соткана из нитей.
Геометрические тела Демокрит считал образованными из параллельных пластинок, толщина каждой из которых равна атому. В Демокритовой атомистической математике все отрезки соизмеримы, но в ней возникают новые противоречия.
Вторым был путь так называемой геометрической алгебры. Были разработаны графические (обычно, приближенные) методы вычисления положительных корней уравнений первой степени и квадратных.
Однако методы геометрической алгебры оказались бессильными перед уравнениями высших степеней. Результаты были приближенными и подавались всегда в форме каких-то геометрических фигур.
Греки первыми стали использовать дроби типа m/n, хотя в IV в. до н. э. еще не было достаточно обоснованной теории введение в науку этих новых математических объектов и теорий операций с ними. Математика уже требовала большего.
Нужна была теория, которая вводила операции, применяемые как к рациональным, так и к иррациональным числам. Только с помощью множества действительных чисел можно обосновать теорию измерения различных величин. Удивляет уже то, что греческие ученые понимали необходимость такой теории.
А Евдокс Книдский построил ее с таким глубоким и логичным совершенством, что все величие его творения поняли только математики конца XIX века. Была разработана теория действительного числа. Выяснилось, что она только терминологией и отдельными деталями отличается от теории отношений Евдокса Книдского.
Метод исчерпывания
С помощью «метода исчерпывания» Евдокс доказал ряд известных, но не обоснованных тогда еще теорем. Его применяли Евклид и Архимед для вычисления площадей, объемов и центров тяжести геометрических фигур.
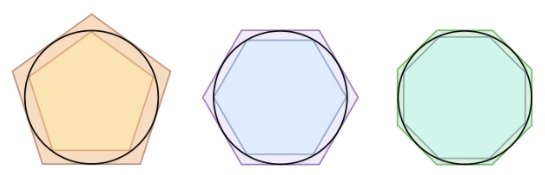
Вычисление площади круга при помощи других фигур — «методом исчерпывания»
Теперь такие задачи решают с помощью интегрального исчисления. Метод Евдокса был скорее методом доказательства известных фактов, чем открытием новых. Вместе с тем это было первое учение о границах. С помощью этого метода можно было вычислять границы широкого класса последовательностей.
Теории Евдокса укрепили теоретические основы математики, положили конец первому замешательству. Это вернуло ученым уверенность в надежности математических теорий.
Друзья, если для вас была полезна статья «Евдокс Книдский: о жизни древнегреческого математика», поделитесь с друзьями в социальных сетях.




